This post contains the content of a talk, titled “A new language for science and philosophy”, that I gave for the Science Cafe at the Faculty of Bioscience Engineering (UGent). This talk was born after reading the book “Modal homotopy type theory: The prospect of a new logic for philosophy” by David Corfield and, although most people in the audience might have felt like they got struck by hammer (a lot of information in an arguably too short time frame), I had a lot of fun preparing and giving it.

Overview

The structure of the talk was as follows:

  • What is typing?
  • Why is it useful?
  • What is type theory?
  • How to incorporate ‘modalities’?
  • What does the future bring?
Typing

Most people have seen two types of programming languages:

  • Weakly typed: variables have no apparent types and weird stuff can happen.
  • Strongly typed: variables have `fixed’ types and operations can only be applied to predetermined types.
Note
In the remainder of the post, static typing is assumed.

An example would be: (type casting is left aside)

Weak typing:

$\mathrm{var}\ a := 5$
$\mathrm{var}\ b := \text{tree}$
$\mathrm{print}(a+b)$

Output: Unknown
Strong typing:

$\mathrm{int}\ a := 5$
$\mathrm{String}\ b := \text{tree}$
$\mathrm{print}(a+b)$

Output: Error!


The main question at this point is probably: “How does this connect to science and philosophy?” Type systems can actually be used to give an alternative approach to:

  • computer science
  • logic
  • mathematics
  • (science) philosophy
  • physics
  • …
Computational Trilogy

An important relation is the so-called computational trinitarianism. It extends the ‘propositions-as-types’ and ‘programs-as-proofs’ paradigms by Curry and Howard.

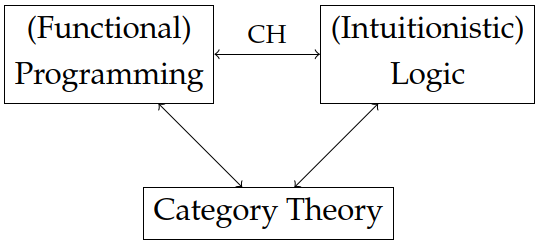
Most programming languages are imperative, i.e. they consist of chains of commands that alter the state of the program. Functional languages on the other hand work in a completely different manner. The commands are replaced by declarations and chains of functions. Church’s $\lambda$-calculus gives a formal model for functional calculus.

In ‘ordinary’ logic, some important assumptions are often lurking in the background, e.g. the axiom of choice or the law of excluded middle. However, these are just axioms! They do not have to hold. Intuitionistic (or constructive) logic is a form of logic where these are weakened, e.g.:

\[\phi\lor\lnot\phi\ \ \text{and}\ \ \lnot\lnot\phi\vdash\phi\ \ \text{do not hold!}\]

As a consequence, to prove a theorem, an explicit proof or construction needs to be provided.

In the post on diagrammatic calculus, the notion of a category was introduced. Some relevant examples are:

  • Sets and functions,
  • vector spaces and linear maps,
  • elements of (partially) ordered sets and order relations between them, and
  • groups represented as one-object categories with group elements as morphisms.
Type Theory

The logical side of the trinity is given by (Martin-Löf) dependent type theory:

  • Propositions, classes, data structures, … are represented by types.
  • Specific proofs, objects or variables are represented by terms (of a given type).

Some examples are:

\[\text{square}:\text{Shape}\qquad 2:\mathbb{N}\qquad\text{LSTM}:\text{Model}\]

The modifier ‘dependent’ indicates that types can depend on other ones. This corresponds to propositions or programs depending on a context.

In contrast to Hilbert-style reasoning, type theory uses natural deduction:

  • Formation: Requirements for defining the type. (Constructor signature)
  • Introduction: Explicit construction of a term. (Constructor implementation)
  • Elimination: How terms can be used. (Function signature)
  • Computation: Explicit implementation of elimination rule for constructors. (Function implementation)

A (simple) example of the natural deduction rules is given by the product type:

  • Formation: $A,B:\mathrm{Type}\vdash A\times B:\mathrm{Type}$,
  • Introduction: $a:A,b:B\vdash (a,b):A\times B$,
  • Elimination: $p:A\times B\vdash \pi_1(p):A,\pi_2(p):B$, and
  • Computation: $a:A,b:B\vdash\pi_1(a,b)\equiv a, \pi_2(a,b)\equiv b$.
Note
A standard problem in formal language modelling is the notion of 'donkey sentences' such as "Every farmer that owns a donkey, beats it". Set-theoretic treatments of such sentences fail without rephrasing the sentence:
  • $\forall x\bigl(\mathrm{isFarmer}(x)\land\exists y\bigl(\mathrm{isDonkey}(y)\land\mathrm{owns}(x,y)\bigr)\rightarrow\mathrm{beats}(x,y)\bigr)$
    The issue here is that $y$ is unbound.

  • $\forall x\bigl(\mathrm{isFarmer}(x)\land\exists y\bigl(\mathrm{isDonkey}(y)\land\mathrm{owns}(x,y)\rightarrow\mathrm{beats}(x,y)\bigr)\bigr)$
    The issue here is that any non-donkey $y$ satisfies this formula.
Type-theoretic model: $$\prod_{z:\Sigma_{f:\mathrm{Farmer}}\Sigma_{d:\mathrm{Donkey}}\mathrm{Beats}(f,d)}\mathrm{Rides}\bigl(\pi_1(z),\pi_1(\pi_2(z))\bigr)\,.$$
Modal Logic

Modal logic is a more subtle form of logic where propositions can hold in a ‘specific way’. For example, in epistemic (or alethic) logic, there exist the necessity $\square$ and possibility $\diamond$ modalities. $\square P$ means that $P$ nececessarily holds and $\diamond P$ means that $P$ possibly holds. These satisfy some conditions such as $\square P\vdash\square\square P$ and $\square P\vdash P$.1

Consider two functors $F:\mathbf{C}\rightarrow\mathbf{D}$ and $G:\mathbf{D}\rightarrow\mathbf{C}$, i.e. maps between categories that send objects to objects and morphisms to morphisms. These are said to be adjoint if morphism are mapped in a bijective manner, i.e. $$\mathbf{D}(Fc,d)\cong\mathbf{C}(c,Gd)\,.$$ This relation is denoted by $F\dashv G$.

A simple example of adjoint functors is given by a Galois connection such as that formed by quantile functions and CDFs:

\[Q(x)\leq y\qquad\iff\qquad x\leq F(y)\,.\]

For (partially) ordered sets, an arrow $x\rightarrow x’$ corresponds to an ordering $x\leq x’$. Another example is given by currying:

\[\mathrm{Func}(A\times B,C)\cong\mathrm{Func}\bigl(A,\mathrm{Func}(B,C)\bigr)\,.\]

Functions from a product set are equivalent to parametrized functions.

Recall the notion of a monad. When $F\dashv G$ are adjoints, the composite $G\circ F$ is a monad (the other composite $F\circ G$ is a so-called comonad). An example of a monad that arises as the composition of adjoint functors is the List monad.2 This monad assigns to a set $S$ the set of all lists over it:

  • $\mathrm{List}\,S := \{\text{all lists of elements of }S\}$.
  • $\mathrm{List}\,f$ applies $f:S\rightarrow T$ to all elements of a list.
  • $\eta_S$ creates singleton lists: $x\mapsto (x)$.
  • $\mu_S$ flattens nested lists: $((a),(b),(x, y, z))\mapsto(a,b,x,y,z)$.

Motivated by Hegel’s “Wissenschaft der Logik”, Lawvere axiomatized parts of logic and philosophy using adjoint modalities. Adjoints resemble and can be used to formalize the idea of oppositions (thesis and antithesis). The possibility $\circ$ and necessity $\diamond$ from epistemic logic form a good example here. (The monad morphisms correspond to the axioms of S4 modal logic.) Another example is the Hegelian opposition of nothing and pure being:

\[\emptyset\dashv\ast\,.\]

The functor $\emptyset$ sends any set to the empty set and $\ast$ sends any set to ‘the’ one-element set ${\ast}$. As for every adjoint, the (co)unit morphisms for any set $X$ can be put in a sequence:

\[\emptyset\rightarrow X\rightarrow\{\ast\}\,.\]

This corresponds to Hegel’s quote “There is nothing which is not an intermediate state between being and nothing.”

Certain categories admit a chain of adjoints. Consider the situation of geometric structures:

\[\mathrm{Disc}\dashv\Gamma\dashv\mathrm{coDisc}\,,\]

with the outer functors going from sets to ‘geometric spaces’ (e.g. manifolds or topological spaces) as follows:

  • $\mathrm{Disc}$ creates spaces with discrete structure (no cohesion).
  • $\Gamma$ sends a space to its ‘underlying set’ of points.
  • $\mathrm{coDisc}$ creates spaces with codiscrete structure (a blob).

These induce adjoint modalities

\[\flat\dashv\sharp := \mathrm{Disc}\circ\Gamma\dashv\mathrm{coDisc}\circ\Gamma\,.\]

By considering spaces with more structure, such as superspaces or infinitesimal spaces, even longer chains can be found. The induced modalities encode many important phenomena such PDEs, differential operators, differential geometry, …

HoTT

The motivating example is (classical) homotopy theory. Consider the following lines:

These lines are equal up to continuous deformations. They are ‘equal’ for many (mathematical) purposes. Two curves not being homotopic gives us information about global structures such as holes, disconnected pieces, …

Homotopy is relevant for type theory through the following observation. For any type $A:\mathrm{Type}$, there exist identity types:

\[a,a':A\vdash (a=_Aa'):\mathrm{Type}\,.\]

But there also exist equivalences (isomorphisms, homotopies, weak equivalences, …):

\[a,a':A\vdash (a\simeq_Aa'):\mathrm{Type}\,.\]

The univalence axiom says that

\[(a=_Aa')\simeq_\mathrm{Type}(a\simeq_Aa')\,.\]

This axiom establishes the homotopic nature of the theory! But what about iterated identity types $p=_{a=_Aa’}q$? Diagramatically these are given by:

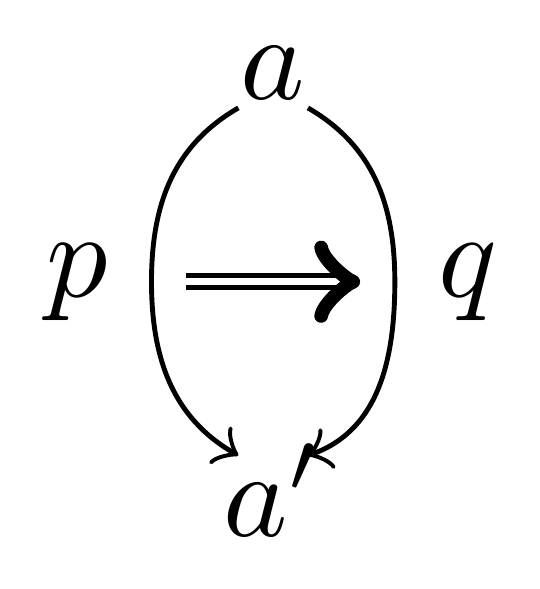
As in the section on higher dimensions in the study of diagrammatic calculus, these higher diagrams induced by iterated identity types also indicate that we should pass from ordinary category theory to $\infty$-category theory (or, when including logic, $\infty$-topos theory). If the identities/equivalences are seen as morphisms between objects, higher identities can be seen as morphisms between morphisms (and so on). These are called $n$-morphisms in higher category theory. If all higher morphisms are equivalences, an $(\infty,1)$-category is obtained. The term ‘topos’ indicates that one can treat the objects in the category as some kind of generalized set.

For modern physics and geometry, some extra ingredients are required on top of mere sets:

  • Spaces of physical objects (particles, fields, …),
  • Locality: the physical behaviour only depends on local information, and
  • Gauge principle: two indistinguishable objects are not necessarily identical (symmetries do not necessarily act trivially in the mathematical formalism).

Combining these requirement leads to the following structures:

  • Locality implies that the objects are sheaves and, more generally, ($\infty$-)stacks.
  • Gauge principle implies that these are valued in ($\infty$-)groupoids, i.e. the symmetry transformations are invertible up to higher equivalences.

These objects form the prototypical example of an $(\infty,1)$-topoi.

Consider the category $\mathbf{Set}$. For every proposition $P$ about elements of a set $S$, there exists a characteristic function $\chi_P:S\rightarrow{0,1}$. This gives the function space $\mathrm{Func}\bigl(S,{0,1}\bigr)$ the structure of a Boolean algebra and, hence, it has a form of logic. For $(\infty,1)$-topoi there exists a similar (internal) logic: homotopy type theory! For example, if the objects are chosen to form a suitable generalization of vector spaces and linear algebra, a language for quantum computing is recovered.

References
  • Corfield, David. (2020). Modal homotopy type theory: The prospect of a new logic for philosophy. Oxford University Press.
  • The Univalent Foundations Program. (2013). Homotopy type theory: Univalent foundations of Mathematics. Institute for Advanced Study.
  • $n$Lab
  • Many years of struggling.
Footnotes

  1. An interpretation of these operators is given by Kripke’s possible world semantics. ↩

  2. The adjoint functors are the forgetful functor, which sends a monoid to its underlying set, and the free monoid functor, which sends a set to its free monoid. ↩