This post contains the content of a talk, titled “Drawing pictures with Nico”, that I gave for the Statistics Discussion Group at the Faculty of Bioscience Engineering (UGent). I have reworked parts of the talk and elaborated on many concepts. Moreover, I have added an ‘optional’ part at the end which puts everything within a much more abstract setting.

Overview

The structure of the talk was as follows:

  1. Short introduction on probability theory,
  2. Diagrammatic methods for Markov categories,
  3. Rigidity for finite sets,
  4. Contexts as categories, and
  5. Geometric ideas for higher mathematics.
Probability

In most (applied) courses on probability theory and statistics, the definition of a probability distribution is given for either the case of finite sets or Euclidean spaces, without explicitly referencing the underlying structure. Moreover, many subtleties and possible problems are ignored. For a more complete introduction, see the appendix on measure theory.

The first part of the talk consisted of a formal treatment by first considering the notion of event, and only then, introducing the collection of distributions compatible with these events. For an arbitrary set $\mathcal{X}$, a good choice of events, called measurable subsets, is given by the notion of $\sigma$-algebras.

There exist two trivial examples:

  • The trivial $\sigma$-algebra: $\Sigma_\text{trivial}:=\{\emptyset,\mathcal{X}\}$, and
  • The discrete $\sigma$-algebra: $\Sigma_\text{disc}:=2^\mathcal{X}$.

The latter is, for example, the one used in the definition of discrete distributions. Note that these collections can be defined on any set, they do not use any structure on $\mathcal{X}$. On these $\sigma$-algebras, we can then define the notion of (probability) measure (or distribution). An important probability measure for this talk is the Dirac measure:

\[\delta_x(A) := \mathbb{1}_A(x) = \begin{cases} 0&\text{if }x\not\in A\,,\\ 1&\text{if }x\in A\,. \end{cases}\]

As with most mathematical structures, we like to consider functions that preserve the given structure. For measurable spaces, the correct notion is that of a measurable function. The reason for using the preimage has to do with the definition of events. Disjoint unions are not preserved under (direct) images.

Note
Equip the set of probability measures $\mathbb{P}(\mathcal{X})$ with the measurable structure generated by the evaluation functionals $$\mathrm{ev}_A:\mathbb{P}(\mathcal{X})\rightarrow\mathbb{R}:P\mapsto P(A)$$ for all events $A\in\Sigma$. Since every measurable function $f:(\mathcal{X},\Sigma_\mathcal{X})\rightarrow(\mathcal{Y},\Sigma_\mathcal{Y})$ sends probability measures to probability measures: $$f_*:\mathbb{P}(\mathcal{X})\rightarrow\mathbb{P}(\mathcal{Y}):P\mapsto P\circ f^{-1}\,,$$ the operation $\mathbb{P}$, which sends measurable spaces to sets of probability measures and functions to pushforwards, obtains the structure of a monad, the Giry monad.
Consider two measurable spaces $(\mathcal{X},\Sigma_\mathcal{X})$ and $(\mathcal{Y},\Sigma_\mathcal{Y})$. A Markov kernel $\mathcal{X}\rightarrow\mathcal{Y}$ is a function $f:\Sigma_\mathcal{Y}\times\mathcal{X}\rightarrow[0,1]$ such that:
  1. For every $A\in\Sigma_\mathcal{Y}$: $x\mapsto f(A\mid x)$ is measurable.
  2. For every $x\in\mathcal{X}$: $A\mapsto f(A\mid x)$ is a probability measure.
More concisely, a Markov kernel is a measurable function $\mathcal{X}\rightarrow\mathbb{P}(\mathcal{Y})$. If the second condition is relaxed to only requiring $f(\cdot\mid x)$ to be a measure, the notion of a transition kernel is obtained.

Some examples of kernels are:

  1. Random walk: $p(i\mid j) := p\delta_{i,j+1} + (1-p)\delta_{i,j-1}$
  2. Identity function: $\mathbb{1}(i\mid j) := \delta_{i,j}$
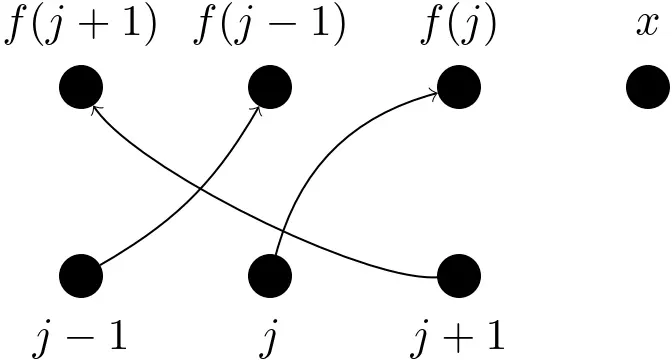
  3. Measurable function: $f(i\mid j) := \delta_{i,f(j)}$

Integration (against a probability measure) will not be introduced in detail (even though it was necessary for this talk). Suffice it to say that it reduces to summation in the case of point masses (and discrete distributions) and to ordinary (Riemann) integrals in the case of density functions.

Diagrams

The basic ingredients of any diagram are lines (or arrows):

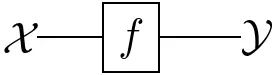
The convention in this post is that diagrams have to be read from left to right. The interpretation of arrows depends on the context:

  • Set theory: functions $X\rightarrow Y$,
  • Linear algebra: linear maps $X\rightarrow Y$, or
  • Probability theory: Markov kernels $X\rightarrow\mathbb{P}(Y)$.

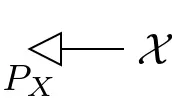
Probability measures, also called states in this setting, are arrows out of the one-element set $\mathbf{I}:=\{\ast\}$:

Joint states are simply indicated by multiple outgoing lines:

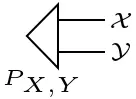
Given the above information, the context for a diagrammatic calculus can be fixed. The following notations will be used in the remainder:

  • Set: Sets and ordinary functions,
  • Vect (technically FinVect): (Finite-dimensional) vector spaces and linear maps,
  • Meas: Measurable spaces and measurable functions,
  • $\mathbf{Stoch}$: Probability spaces and Markov kernels,
  • $\mathbf{BorelStoch}$: Borel probability spaces and Markov kernels, or
  • $\mathbf{FinStoch}$: Finite probability spaces and Markov Kernels.

Concatenation of lines or arrows is, in general, given by a suitable notion of composition:

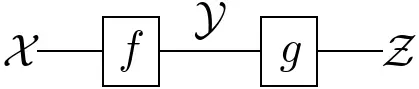
The interpretation, again, depends on the context:

  • Set, Vect & Meas: function composition $g\circ f$, or
  • $\mathbf{Stoch}$: Chapman–Kolmogorov equation \[(g\circ f)(A\mid x) :=\int_\mathcal{Y}g(A\mid y)\,df(y\mid x)\,.\]

Lines or arrows can also be combined in different ways:

  • Parallel functions: $f\otimes g:\mathcal{X}\otimes\mathcal{X}’\rightarrow\mathcal{Y}’\otimes\mathcal{Y}’$
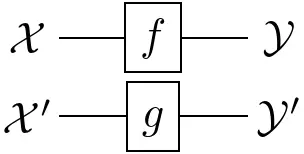
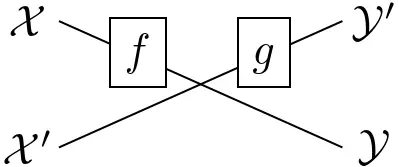
  • ‘Braided’ functions: $x\otimes x’\mapsto g(x’)\otimes f(x)$

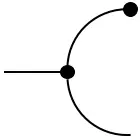
Every measurable space $(\mathcal{X},\Sigma_{\mathcal{X}})$ admits two `structure morphisms’:

  • The deletion map: $\mathrm{del}_\mathcal{X}(x) := 1$

    which corresponds to integrating out a variable: $\displaystyle\int_\mathcal{Y}df(y\mid x)$

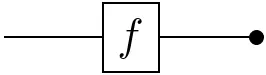
  • The copy map: $\mathrm{copy}_\mathcal{X}(A\times B\mid x) := \delta_x(A)\delta_x(B)$

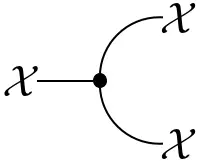
    which corresponds to transporting a distribution on $\mathcal{X}$ to one on its diagonal embedding in $\mathcal{X}\otimes\mathcal{X}$.

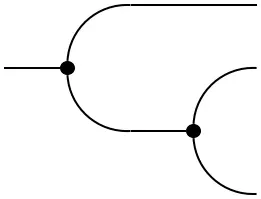
These morphisms endow a probability space with the structure of an (internal) comonoid:

=

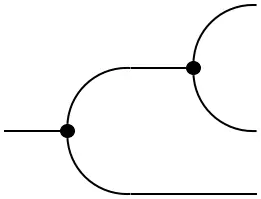and

= =

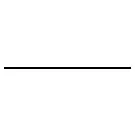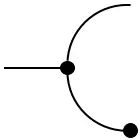
The idea behind comonoids can be understood by turning these diagrams around (i.e. ‘inverting time’). The first equation is then simply the associativity of a multiplication map and the second equation is the unit law. (Sets with a multiplication map with these properties are also called monoids.) Such ‘dual’ definitions are a common occurrence in abstract parts of mathematics. It is a nice intuition to have!

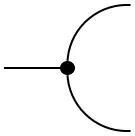
Probability spaces are even (co)commutative comonoids:

=

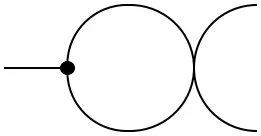More generally, contexts $\mathbf{C}$ where the structure morphisms $\mathrm{del}$ and $\mathrm{copy}$ exist and satisfy the (co)commutative comonoid conditions are called Markov categories or copy-discard (CD) categories.

Every set admits a unique comonoid structure with respect to the Cartesian product (which can also be thought of as a tensor product for which the unit is the one-element set $\mathbf{I}$):

  • Delete morphism: unique function to $\mathbf{I}$.
  • Copy morphism: diagonal embedding $x\mapsto(x,x)$. Vector spaces do not admit this diagonal comonoid structure. Can you see why? (In physics, this gives rise to the no-cloning theorem!)

Using the above diagrammatic rules, various notions from probability theory can be represented. Some examples will be covered below.

A deterministic function should always give the same result for a fixed input. Diagrammatically this corresponds to:
=
An interesting question becomes: Are all deterministic functions in $\mathbf{Stoch}$ given by measurable functions? The answer is no in general! There are pathological counterexamples. However, the statement is true for $\mathbf{BorelStoch}$ and $\mathbf{FinStoch}$.
If for all functions $f,g$ and $h_1,h_2$, the relation
=
implies
=
then the context $\mathbf{C}$ is said to be causal.
The definition of conditional distributions in $\mathbf{Stoch}$ reads as $$P(A,B) = \int_A P(B\mid x)\,dP(x)\,.$$ Diagrammatically, for any context $\mathbf{C}$, this becomes:
=
The existence of conditionals is a subtle point. In $\mathbf{Stoch}$, conditionals coincide with the notion of regular conditional distributions. However, these do not exist for all joint distributions. When restricting to $\mathbf{BorelStoch}$ or $\mathbf{FinStoch}$, the situation is better behaved: all conditionals exist.

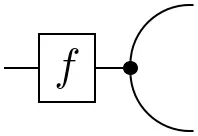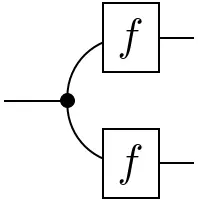
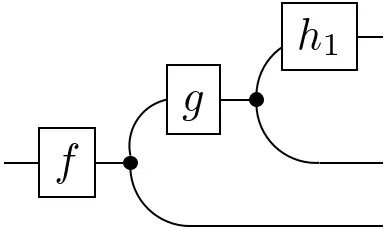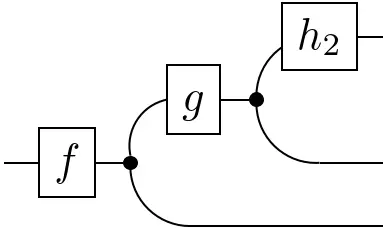
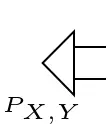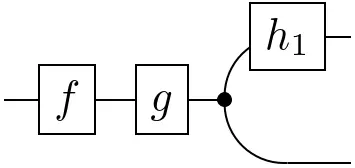
When working with states (or functions) of higher arity, e.g. a joint state on three variables, conditioning can be done in different ways. By 'simple' diagrammatic manipulations, the following property can be proven whenever $\mathbf{C}$ has all conditionals:
=
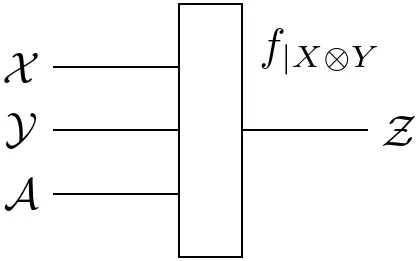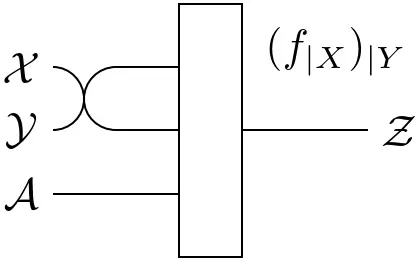
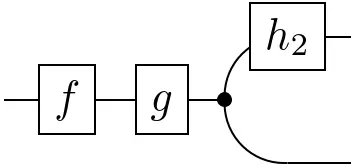
Just for fun, this is left as an exercise to the reader ;-)

Note that the definition of conditionals is not reserved to states $\mathbf{I}\rightarrow\mathcal{X}\otimes\mathcal{Y}$. It can be generalized to arbitrary functions $\mathcal{Z}\rightarrow\mathcal{X}\otimes\mathcal{Y}$:
=
Two functions $f,g:\mathcal{Y}\rightarrow\mathcal{Z}$ are said to be $p$-almost surely equal, for a function $p:\mathcal{X}\rightarrow\mathcal{Y}$, if $$f\circ p=g\circ p\,.$$ Diagrammatically this becomes:
=
Let $\mathbf{C}$ be a causal context admitting all conditionals. Define a context Stoch(C) for which a probability space in $\mathbf{C}$ is a pair $(\mathcal{X},\psi)$ such that $\mathcal{X}$ is an object in $\mathbf{C}$ and $\psi:\textbf{I}\rightarrow\mathcal{X}$ a state, and for which a kernel $(\mathcal{X},\psi_X)\rightarrow(\mathcal{Y},\psi_Y)$ is a function $f:\mathcal{X}\rightarrow\mathcal{Y}$ in $\mathbf{C}$ such that $\psi_X$-almost surely $f\circ\psi_X=\psi_Y$. If $\textbf{C}=\textbf{Stoch}$, then Stoch(C) is given by the context of 'couplings' (or copulas), i.e. that of probability spaces and joint distributions that restrict to two given marginals.
Finite Sets

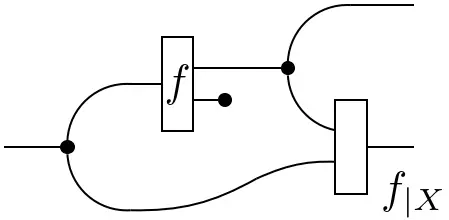
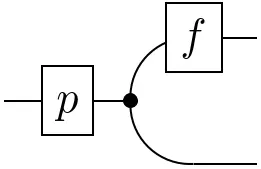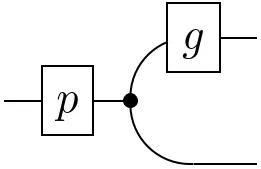
From here on, attention will be restricted to finite sets, i.e. we work in $\mathbf{FinStoch}$ (unless stated otherwise). These will be equipped with the discrete $\sigma$-algebra. In this case, (probability) measures are defined by their values at points and can be written as vectors. Moreover, kernels can be expressed as matrices. To allow for some more diagrammatic freedom, functions are generalized from Markov kernels to transition kernels, where the latter need only take values in the set of measures (which can be unnormalized).

Every object $(\mathcal{X},\Sigma_{\mathcal{X}})$ admits the structure of an (internal) monoid:

  • Unit map: $\varepsilon_\mathcal{X}(x) := 1$
  • Multiplication map: $\mu_\mathcal{X}(x\mid i,j) := \delta_{i,x}\delta_{j,x}$

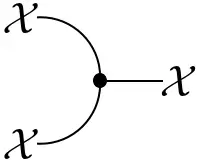
As before, this structure is commutative with respect to the (trivial) braiding. As noted in the previous section, the definition of a comonoid was dual to that of a monoid. This is clear when comparing the explicit formulas for the comultiplication and counit to the expressions above. The multiplication $\mu$ and unit $\varepsilon$, consequently, also satisfy the associativity condition and unit law. Finite probability space not only carry the structure of a monoid and comonoid, they are even compatible in an elegant way. Such objects are called Frobenius monoids:

= =
The multiplication map allows us to turn states into arrows:
=
The state can then be recovered through the unit map:
=
An inverse modifier is simply a functional inverse to a modifier:
= =
These are given as follows: $$X^{-1}(i\mid j) = \frac{1}{X(i\mid j)} = \frac{\delta_{i,j}}{P_X(i)}\,.$$ Further below, inverse modifiers will be used to express conditionals more explicitly.

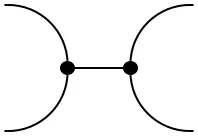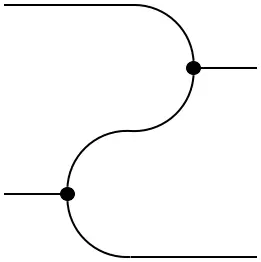
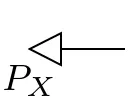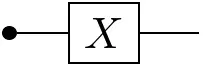
Using the different structures on a finite probability space $(\mathcal{X},\Sigma_{\mathcal{X}})$, even more diagrammatic objects can be obtained:

  • Cups:
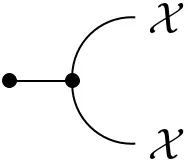    = $\mathrm{coev}_\mathcal{X}(x,x') = \delta_{x,x'}$
  • Caps:
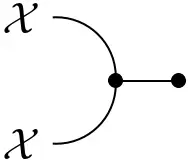    = $\mathrm{ev}_\mathcal{X}(x,x') = \delta_{x,x'}$

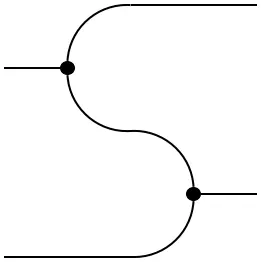
The cup and cap give rise to a so-called rigid structure (see further below) because they satisfy the triangle identities or yanking conditions:

= =

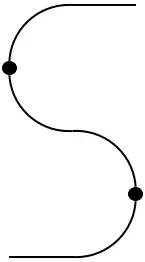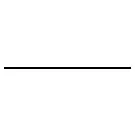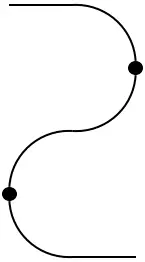
The reason for the term ‘yanking condition’ stems from the fact that the bends in the lines can be ‘yanked out’.

Although the diagonal comultiplication does not exist for vector spaces, a rigid structure exists on finite-dimensional vector spaces. For a vector space $V$, choose a basis $\{e_i\}_{i\leq\dim(V)}$ and denote its dual basis by $\{e^i\}_{i\leq\dim(V)}$.

  • Cup: $\mathrm{coev}_V(\lambda) := \sum_{i=1}^{\dim(V)}\lambda e^i\otimes e_i$.
  • Cap: $\mathrm{ev}_V(e_j\otimes e^i) := e^i(e_j) = \delta^i_j$.

As an example of diagrammatic calculus, the ‘bubble diagram’ gives the dimension of the vector space (more generally, the trace of a linear map):

= $\sum_{i=1}^{\dim(V)} e^i(e_i) = \sum_{i=1}^{\dim(V)}\delta^i_i = \dim(V)\,.$

These constructions, and their extensions to superspaces, are also of importance in theoretical physics! (I might write more about this in a future post.)

Using the cup and cap, we can also express the transposition of linear maps:

=

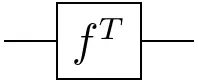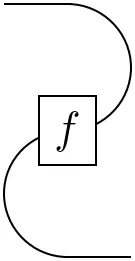
Again, the proof is left as an exercise to the reader. It can easily be obtained using the expressions introduced above ;-)

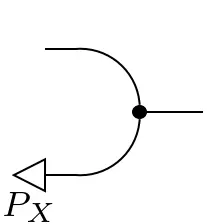
The cups and caps of finite probability spaces can be altered using the (inverse) modifiers:

=

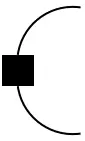and

=

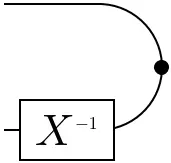
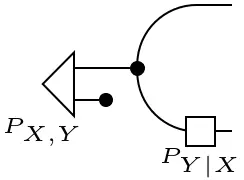
With the modified caps, the conditionals can be given a more explicit expression, which closely resembles the equational definition:

=

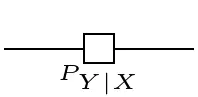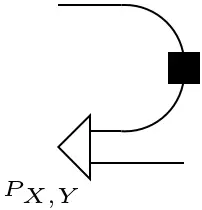
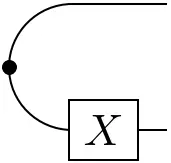
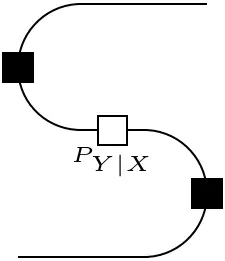
In the context of linear algebra, it was shown how the cups and caps allow us to express transposition by bending lines around. Using the modified cups and caps, transposition of a conditional in $\mathbf{FinStoch}$ gives Bayes’ theorem:

=
Abstract Nonsense

The previous sections should have given an idea of how diagrammatic tools can be used to study vastly different areas of mathematics and science. The reason that this is possible is not a mere coincidence. What were called ‘contexts’ and, more specifically, the specific contexts that were considered, all share the same structure. This section aims to introduce the terminology used to describe these structures.

A category $\mathbf{C}$ consists of two collections (in practice, these are often sets):
  1. Objects: $\mathrm{ob}(\mathbf{C})$, and
  2. Morphisms: $\mathrm{hom}(\textbf{C})$.
The collection of morphisms between two object $X,Y\in\mathrm{ob}(\mathbf{C})$ is denoted by $\hom_{\mathbf{C}}(X,Y)$ or $\mathbf{C}(X,Y)$. Morphisms $f\in\mathbf{C}(X,Y)$ are represented by arrows or lines and concatenation of lines corresponds to composition of morphisms. Hence, for the most basic diagrams, only the structure of a category is required.

These should satisfy the following conditions:
  1. Identity: For all $X\in\mathrm{ob}(\mathbf{C})$, there exists an identity morphism $\mathbb{1}_X\in\mathbf{C}(X,X)$.
  2. Associativity: $f\circ(g\circ h) = (f\circ g)\circ h$, whenever the compositions are well-defined.

Some examples were already given after the introduction of ‘lines’. Some more exotic examples are (the first 2/3 are a good exercise for drawing diagrams):

  • Every poset (partially ordered set) is a category, where a unique morphism $x\rightarrow y$ exists whenever $x\leq y$.
  • Every directed graph defines a category. (The free category generated by that graph.)
  • The category Cat of small categories, i.e. those where $\mathrm{ob}(\mathbf{C})$ and $\mathrm{hom}(\mathbf{C})$ are sets. (The morphisms are defined below.)
  • The representations of a (finite) group with intertwiners (equivariant functions) as morphisms.

Just as there are functions between sets, there are also operations between categories.

An operation $F:\mathbf{C}\rightarrow\mathbf{D}$ between categories such that:
  1. $F$ maps objects $X$ to objects $FX$.
  2. $F$ maps morphisms $X\rightarrow Y$ to morphisms $FX\rightarrow FY$.
  3. $F$ preserves composition.

The Giry monad that assigns probability measures to measurable spaces was the first example of a functor. Some other examples are:

  • The power set functor $P:\textbf{Set}\rightarrow\textbf{Set}$, which assigns power sets and (pre)images.
  • The Yoneda embedding of an object $X\in\mathrm{ob}(\mathbf{C})$, which assigns to every other object $Y\in\mathrm{ob}(\mathbf{C})$ the morphisms $\mathbf{C}(Y,X)$. Morphisms $f$ are mapped to precompositions $-\circ f$.

The second example is one of the most foundational constructions in category theory!

We can also define morphisms $\kappa:F\Rightarrow G$ between functors.

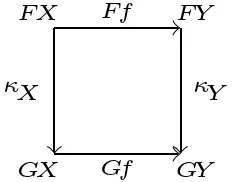
A natural transformation $\kappa:F\Rightarrow G$ is a collection $\\{\kappa_X:FX\rightarrow GX\\}_{X\in\mathrm{ob}(\mathbf{C})}$ of morphisms such that the following commutative diagram holds for any two objects $X,Y\in\mathrm{ob}(\mathbf{C})$:
These transformations are also sometimes denoted by generic indices: $\kappa_X:FX\rightarrow GX$.

Some (technical) examples are (some other examples will pop up in the next few sections):

  • The identity natural transformation $F\Rightarrow F$.
  • Double duals: there exists a natural transformation $\eta_{V}:V\rightarrow V^{**}$ for finite-dimensional vector spaces. (For the single dual $V\rightarrow V^*$, the transformation is ‘unnatural’ since it requires a choice of basis.)
  • For any morphism $f:X\rightarrow Y$ there exists a natural transformation between the Yoneda embeddings of $X$ and $Y$. This is given by postcomposition $f\circ -$.

Whereas objects are represented by vertices and morphisms by lines in a diagrammatic calculus, natural transformations could be represented by filling in the area between two parallel functors (parallel here means that they have the same domain and codomain). This extension of diagrams to higher-dimensional structures will play a role at the end of this talk.

To express parallel objects and morphisms, the structure of a tensor product needs to exist.

A category $\mathbf{C}$ equipped with a (bi)functor $\otimes:\mathbf{C}\times\mathbf{C}\rightarrow\mathbf{C}$ and a unit object $\mathbf{I}\in\mathrm{ob}(\mathbf{C})$ satisfying the monoid conditions:
  1. Associativity: $X\otimes(Y\otimes Z)=(X\otimes Y)\otimes Z$\pause, and
  2. Unit: $X\otimes\mathbf{I}=X=\mathbf{I}\otimes X$.
In general, the associativity and unit conditions can be weakened up to a natural transformation. This will be reconsidered at the end.

In some monoidal categories, the tensor product is symmetric in a certain sense.

A natural transformation $\sigma_{X,Y}:X\otimes Y\rightarrow Y\otimes X$. If $\sigma_{X,Y}\circ \sigma_{Y,X}=\mathbb{1}_{Y\otimes X}$, the braiding is said to be symmetric.
= =
An example of a monoidal category that is not symmetric is given by the braid category. (This is basically the category generated by lines and crossings.)

For cups and caps, another structure is required.

A monoidal category $\mathbf{C}$ such that for every object $X\in\mathrm{ob}(\mathbf{C})$ there exists a dual $X^*\in\mathrm{ob}(\mathbf{C})$ together with two natural transformations $\mathrm{coev}_X:\mathbf{I}\rightarrow X^*\otimes X$ and $\mathrm{ev}_X:X\otimes X^*\rightarrow\mathbf{I}$ satisfying the yanking conditions. A category for which rigidity fails to hold, although duals exist in the algebraic sense, is that of infinite-dimensional vector spaces. (Can you figure out why?)

It is time to relate the categorical notions to the sections on probability theory. Only one piece of data is still missing.

An object $1\in\mathrm{ob}(\mathbf{C})$ such that for every other object $X\in\mathrm{ob}(\mathbf{C})$, there is a unique morphism $X\rightarrow1$.

Putting everything together gives the central object of ‘categorical probability theory’.

A symmetric monoidal category with terminal monoidal unit such that every object admits the structure of an internal commutative comonoid.

To model morphisms such as Markov kernels, some more structure is needed.

Consider a monad, i.e. a functor $T:\mathbf{C}\rightarrow\mathbf{C}$ with multiplication $\mu:T^2\Rightarrow T$ and unit $\mu:\mathrm{id}\Rightarrow T$ (which satisfy the dual diagrammatic properties of comonoids). The Kleisli category $\mathrm{Kl}(T)$ has:
  1. Objects: $\mathrm{ob}\bigl(\mathrm{Kl}(T)\bigr):=\mathrm{ob}(\mathbf{C})$, and
  2. Morphisms: $\hom_{\mathrm{Kl}(T)}(X,Y):=\hom_{\mathbf{C}}(X,TY)$.
The morphisms $X\rightarrow TY$ are called Kleisli morphisms $X\rightarrow Y$. When $T=\mathbb{P}$ is the Giry monad, the Kleisli morphisms are exactly the Markov kernels.

All this data probably looks rather scary and technical (it is). However, it is more useful than it might appear. Many effects in computer science can be modelled using monads and Kleisli morphisms. Almost any process with ‘side effects’ such as I/O operations can be modelled using a monad. (People that use Haskell love this stuff.)

If $\mathbf{C}$ is a Markov category and $T:\mathbf{C}\rightarrow\mathbf{C}$ is a monad that preserves the product and unit, $\mathrm{Kl}(T)$ is again a Markov category. Moreover, on any Cartesian monoidal category, i.e. a category where the monoidal structure is given by the Cartesian product such as in $\mathbf{Set}$, every object has a unique comonoid structure (diagonal embedding $\mu:x\mapsto x\times x$). The Giry monad $\mathbb{P}$ preserves this structure and, hence, induces a Kleisli category $\mathrm{Kl}(\mathbb{P})$ that is Markov. This is exactly the category $\mathbf{Stoch}$ of Markov kernels from before (hence the name).

Higher Dimensions

(Small) Categories can be built up geometrically from triangles. This follows from the fact that for any two composable morphisms, we obtain the following diagram

By pasting all these triangles along shared edges, (small) categories can be represented as simplicial complexes. (A simplex is a higher-dimensional generalization of a triangle.) If instead of being exactly equal, composition is only defined up to some higher-dimensional morphisms, a 2-morphism, the notion of quasicategory is obtained. This corresponds to filling in the triangles:

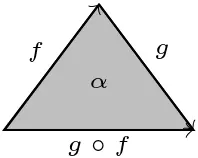
In a similar way, we could fill in pyramids (3-simplices) by 3-morphisms and so on.

Note
This might all sound very exotic, but it is not as crazy as it sounds. Consider for example the setting of quantum mechanics. If $|\psi\rangle$ is the state vector of a system, then $\alpha|\psi\rangle$ represents the same system. Hence, an operator $\mathcal{O}$ might act nontrivially (mathematically), but still give rise to the same physical state, i.e. there exists a 2-morphism $\mathcal{O}\Rightarrow\mathbb{1}$. The possibility of (symmetry) operations acting in a (mathematically) nontrivial way, but giving rise to physically indistinguishable situations has given rise to a rich field (both in physics and mathematics) called gauge theory. Because of these insights and the strong geometric intuition gained in the previous century, people are trying to rewrite and generalize mathematics in geometric (and homotopic) terms. (Some of this will be explained in a future post.)
References
  • Capiński, Marek, and Peter E. Kopp. (2004). Measure, integral and probability. Vol. 14. Springer.
  • Fritz, Tobias. (2020). A synthetic approach to Markov kernels, conditional independence and theorems on sufficient statistics. Advances in Mathematics 370: 107239.
  • Coecke, Bob, and Robert W. Spekkens. (2012). Picturing classical and quantum Bayesian inference. Synthese 186: 651–696.
  • $n$Lab